Our group focuses on integrating the fundamental structure of physics and mathematics into machine learning architectures. By embedding principles from geometric mechanics, exterior calculus, variational methods, and probability into neural networks, we develop models that are both expressive and mathematically grounded in rigorous analysis. This approach allows us to construct machine intelligence systems capable of operating in extreme physical regimes, where traditional first-principles modeling becomes intractable and interpretability is paramount for trustworthy engineering.
We bridge the gap between rigorous mathematics/physics and neural modeling, enabling tools for scientific inference, digital twins, and autonomous experimentation. Our work spans a wide range of multiscale and multiphysics domains—including energy systems, climate science, fusion power, and soft matter. There are deep connections between the geometry belying popular graph learning architectures and the geometric principles in modern finite element methods and geometric approaches to dynamical systems, allowing us to borrow powerful principles from the long tradition of applied mathematics rather than employing empirical tricks.
Here are some themes and techniques that we currently work on:
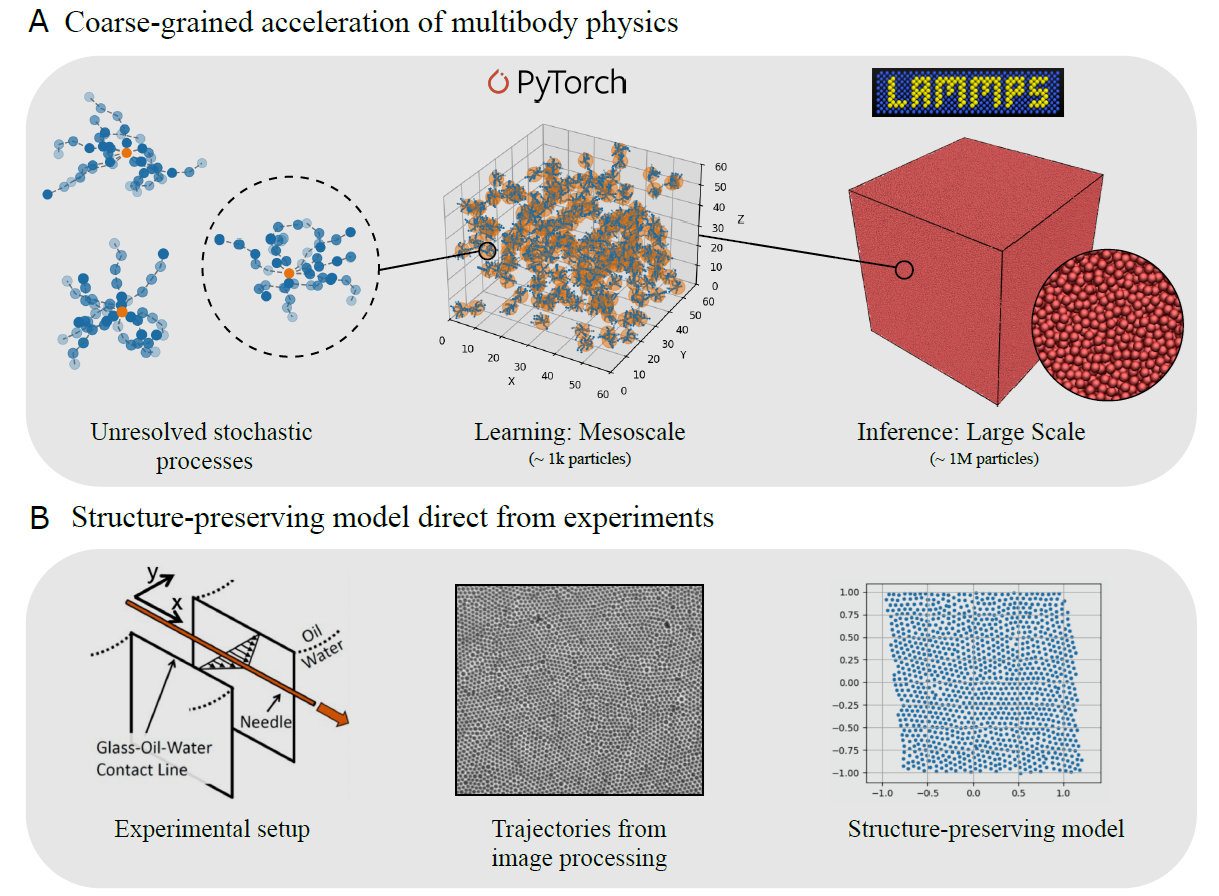Emergent structure from coarse-grained dynamical systems: When high-dimensional dynamical systems, like molecular dynamics or turbulence, are coarse-grained into fast, low-dimensional models, information is lost. This entropy creation manifests as dissipation, stochastic fluctuations and memory effects that lead to emergent stochastic behavior. Geometric frameworks for dynamical systems, including formalisms like Mori-Zwanzig and metriplectic dynamics, provide mathematical language to understand these processes and construct architectures theoretically guarantee we can capture emergent stochastic structure. This allows us to build simulators of massive dynamical systems where inter-agent physics/interactions are simply too complex or slow for first principles modeling.
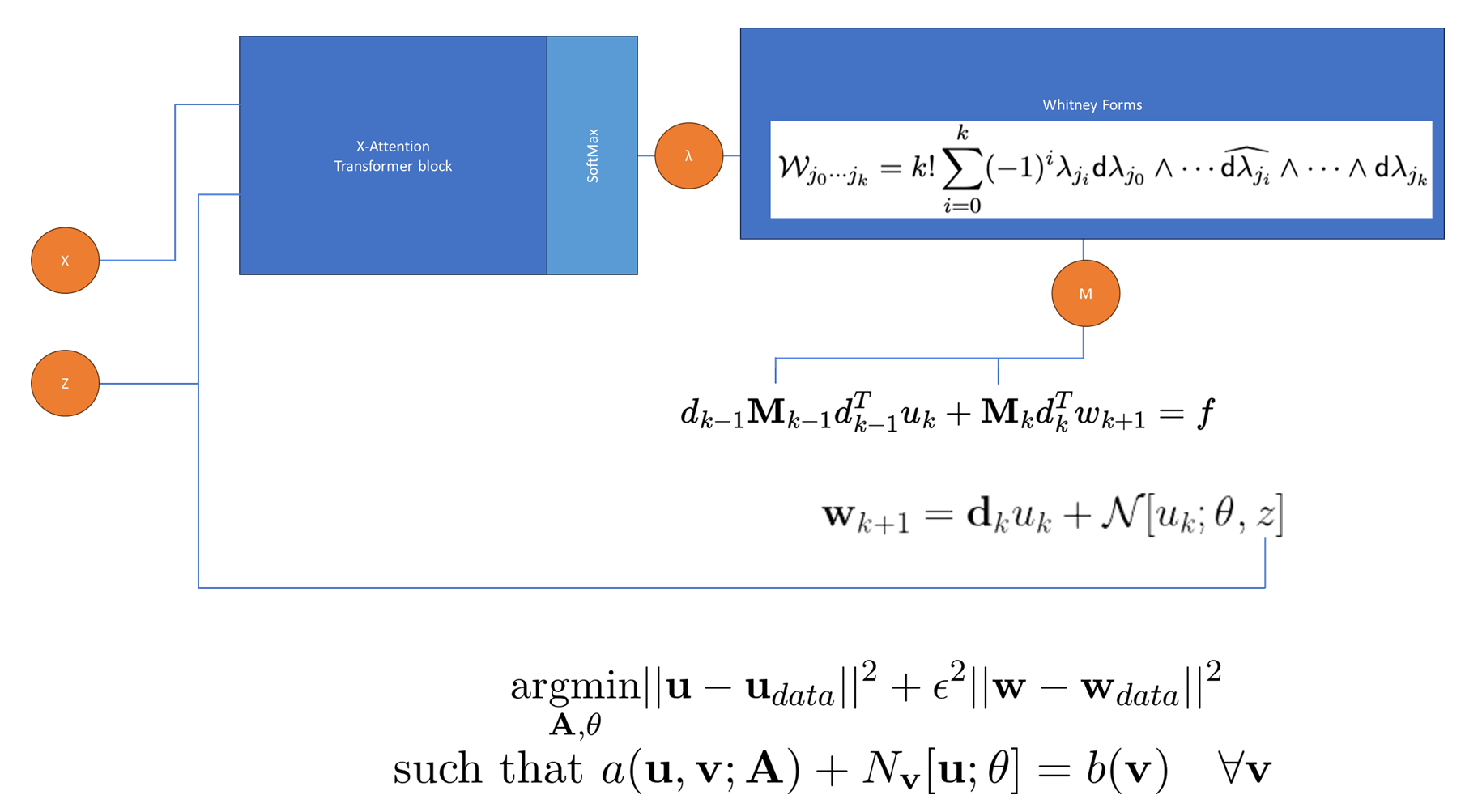Realtime structure-preserving digital twins: With the advent of powerful neural simulators, many aim to build digital twins which can integrate sensor data and make predictions in real time, allowing us to predict and optimally control complex engineering systems. We exploit modern techniques from the finite element exterior calculus to build models which explicitly preserve the geometric structure present in conservation balance equations. These techniques fuse the expressive power of transformer architectures while preserving symmetries and conservation structure, leading to models that can be run in real time while guaranteeing numerical robustness and providing quantified uncertainty. This structure-preservation is particularly crucial to problems in multiscale/multiphysics systems: we consider electromagnetism, fracture mechanics, shock hydrodynamics, hierarchical metamaterials, and other extreme physics that can be antagonistic to “off-the-shelf” physics or ML simulators.
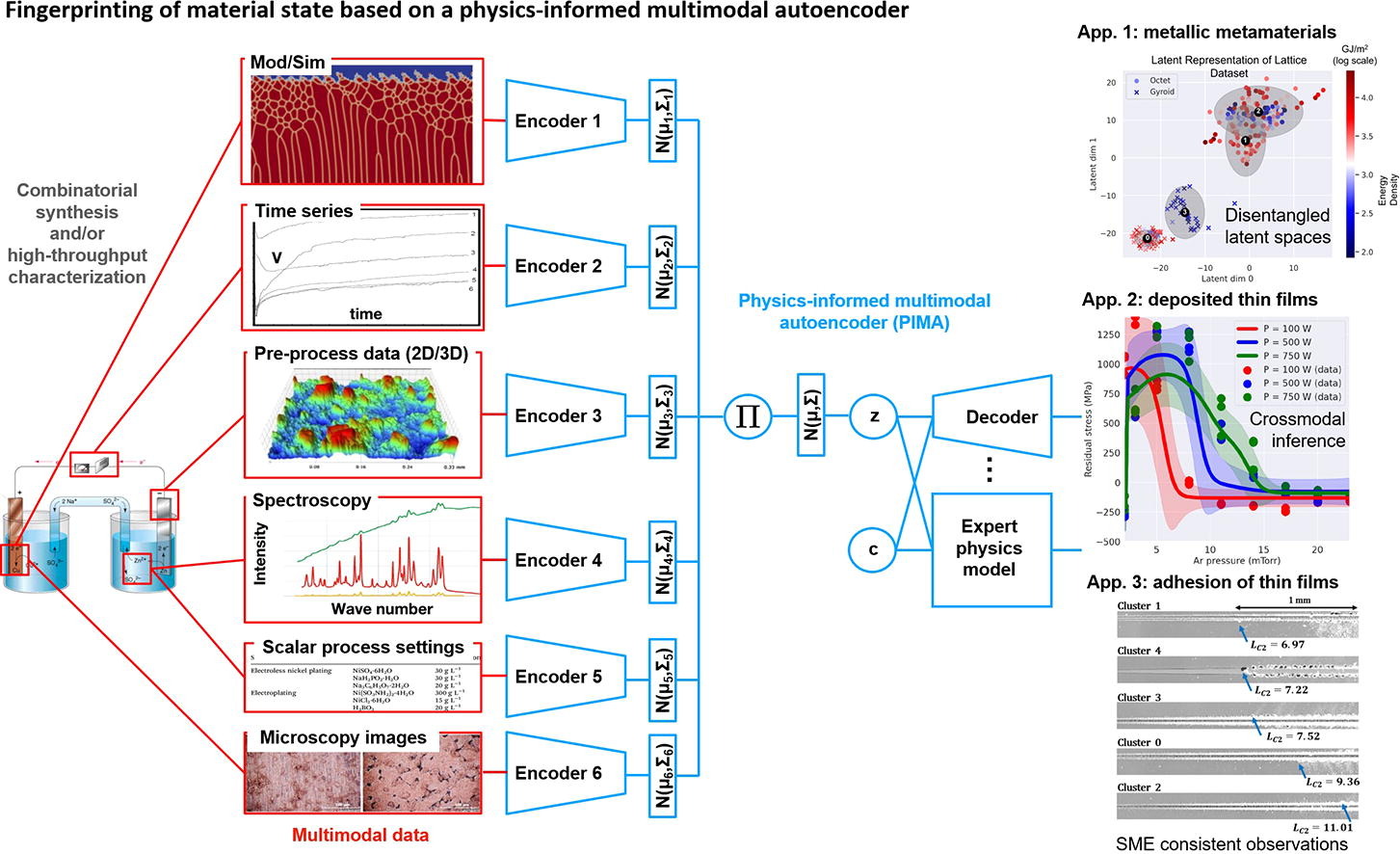Predictive physics from multimodal experiments: Inspired by the success of massive foundation models like ChatGPT, many aspire to build analagous scientific foundation models trained on a large corpus of simulated data. This is fundamentally limited by the throughput of simulation, where the largest supercomputers may be able to generate hundreds of individual simulations, far from the entire internet used to train LLMs. Experimental training data offers a massively higher-throughput path to constructing data, but brings additional challenges. Probabilistic learning schemes must be used to mitigate noise, and measurements are often indirect and multimodal, requiring data fusion or model closure to access the actual fields of interest. This provides a unique interdisciplinary opportunity to design experimental campaigns tailored toward machine learning and using rigorous physical and probabilistic structure to circumvent these challenges. We use these techniques to perform material discovery, to learn models embracing the full complexity of physics of complex systems, and to perform optimal design in realistic settings.
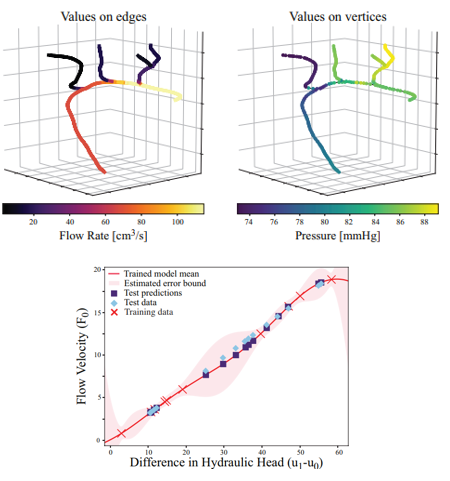Data-driven models with quantified uncertainty supporting verification and validation: A grand challenge for scientific ML models stems from their black-box nature; their expressive power often comes at the price of a model form which is challenging for humans to interpret, concealing the implicit assumptions that determine their range of valid applicability. In high-consequence engineering settings, these models can not be adopted until rigorous error estimates can be provides through uncertainty quantification techniques. Traditional techniques from finite elements don’t naturally map onto deep nonlinear architectures, and so the community is often left with costly sampling techniques or insufficient empirical tricks like dropout. We develop tools based on Bayesian optimization which integrate naturally with the geometric structure, providing probabilistic techniques that naturally estimate errors due to experimental measurement, physical stochasticity, or model form error. This interplay between probability and geometric discretization provides crucial support to the adoption of data-driven models in practical settings, where exploration of worst case scenarios is often more important than nominal performance.
